EBSD Explained
Techniques
Applications
Hints and Tips
Technology
OXFORD INSTRUMENTS EBSD PRODUCTS
CMOS Detector RangeAZtecHKL Acquisition SoftwareAZtecCrystal Processing Software
The collection of the diffraction pattern from the sample is a critical step in the Electron Backscatter Diffraction (EBSD) workflow, but equally important is the process by which that pattern is converted into useful information – namely confirmation of the phase, the 3D orientation of the crystal lattice or subtle changes in the unit cell relative to a reference standard. The EBSD indexing process is at the core of every EBSD system.
However, the requirements from an indexing engine are very dependent on the application in question. For example, for high-speed mapping the focus will be on the indexing of relatively low resolution (and potentially noisy) EBSD patterns in only a few 100 μs whereas for measuring elastic strain, high quality EBSD patterns may need to be compared rigorously to an undistorted reference pattern, with little or no emphasis on speed.
On this page we focus on the techniques used to determine the phase and orientation from EBSD patterns and separate these into 2 broad categories – Hough-transform based techniques and pattern matching techniques, as shown on the tabs below.
Learn more about tools to obtain better quality or new information using advanced analysis techniques, such as high resolution (“HR”) EBSD here.
Conventionally, all automated EBSD indexing approaches have relied on image analysis algorithms that can detect linear features in a relatively noisy image (such as the Kikuchi bands in an EBSD pattern). Since the early work of Krieger Lassen (e.g. Krieger Lassen et al. (1992), “Image processing procedures for analysis of electron back scattering patterns”. Scanning Microsc. 6, 115-121), the Hough transform has been the favoured approach, and this is explained in more detail here.
The Hough transform generates a list of detected band positions, but from this point there are several commonly used approaches to determine the best fit solution to the EBSD pattern. In all cases a theoretical list of the reflectors and their expected intensities needs to be created: this is usually done using kinematical structure factor calculations. The kinematical approach correctly reproduces the geometry of the EBSD patterns, even though it does not enable the creation of realistic pattern simulations. However, for regular Hough-based indexing this is sufficient, and the structure factor calculations (explained in the “Band Intensity” section on the EBSD Pattern Formation page here), are simply used to rank the expected reflectors in terms of their predicted intensities.
From the list of reflectors (with the highest intensities), the software will create a look up table of the angles between the reflector-plane normals, and this is what is then compared to the measured orientations of the Kikuchi bands that have been generated using the Hough transform.
Once the band detection and generation of the reflector look-up table have been created, there are several commonly used approaches to indexing, which are described below.
This approach looks at all the detected Kikuchi bands and compares their interplanar angles with the reflector look-up table. If a coherent match between the two lists of angles is found (within a pre-determined error margin), then that solution has been defined to a reflector group level (i.e. each detected Kikuchi band has been assigned to a particular group of reflectors, such as {111} or {200}). The software will then need to formulate the crystal orientation with respect to the EBSD detector, and store that orientation in a relevant format (such as an orientation matrix or Euler angles).
In general this approach requires fewer detected bands, working well with only 5-8 bands, hence giving good results from structures that give relatively poor patterns. The biggest drawback of the approach is when Kikuchi bands are poorly detected or when the measured EBSD pattern is actually a superposition of 2 overlapping patterns, such as is common at grain and phase boundaries.
This is shown in the below example: a typical high-speed EBSP has been collected at a phase boundary between a ferrite (Body Centred Cubic – BCC – Fe) grain and an austenite (Face Centred Cubic – FCC – Fe) grain. The EBSP contains Kikuchi bands from both of the grains on either side of the boundary, with approximately equal contributions. The full band set indexing approach would almost always detect bands from both structures, most likely resulting in no matching solution.
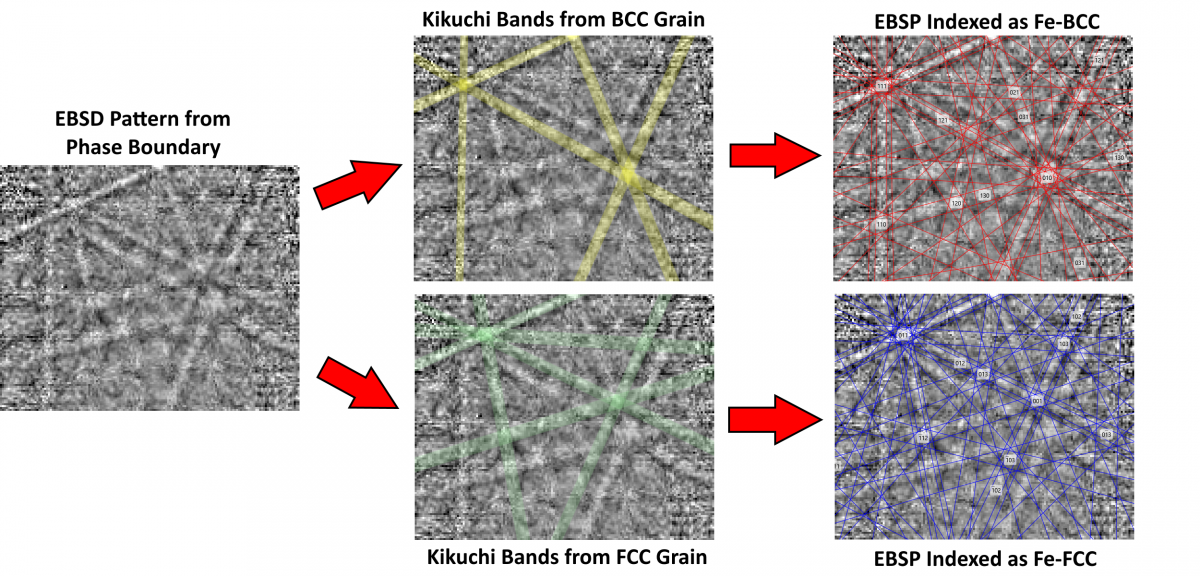
Illustration of the contribution of 2 orientations / phases to a single EBSP. The upper row shows the bands and solution associated with the Fe-BCC grain, the lower row shows the bands and solution associated with the Fe-FCC grain.
The robustness of indexing for EBSPs with overlapping contributions from 2 orientations or phases can be improved by iteratively removing 1 or 2 of the detected bands from the calculations. This improves the likelihood of finding a single solution that fully matches one of the 2 contributing orientations, but would still be unlikely to give a solution in cases where the 2 orientations contribute equally to the final pattern, as shown in the image.
For this reason most commercial EBSD systems break the detected band set down into subsets of 3 or 4 bands, as described below.
Instead of evaluating all of the detected bands from an EBSD pattern as a coherent unit, an alternative approach is to break the list of bands into sets of 3 or 4 (i.e. “triplets” or “quadruplets”). Each of these band subsets can then be used to index the Kikuchi bands down to the reflector group, and then a voting scheme is then used to determine the most likely final solution.
The advantages of this approach over the full band set indexing method described above are numerous:
The main difference between the use of 3 or 4 band groups during the indexing process is the number of combinations of bands that can be utilised for any one EBSD pattern. This is simply a matter of maths, and the table below shows that, if 8 or more Kikuchi bands are detected in the EBSP, then there will be more quadruplets than triplets and hence indexing is likely to be more robust. For EBSD patterns with fewer detectable Kikuchi bands, then triplet indexing is more likely to produce a solution. A more detailed description of the quadruplet approach used in the Oxford Instruments AZtec software (“class indexing”) is provided here.
| Bands: | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Quadruplets: | 5 | 15 | 35 | 70 | 126 | 210 | 330 | 495 |
| Triplets: | 10 | 20 | 35 | 56 | 84 | 120 | 165 | 220 |
Comparison between the number of groups of 3 or 4 bands (triplets and quadruplets) that can be extracted from a set of n detected bands
In recent years, a different approach to EBSD pattern indexing has been developed that does not rely on the detection of the Kikuchi bands using the Hough transform (or similar image processing techniques). This new approach builds on significant developments in the simulation of EBSPs: as described in the section on Hough-based indexing techniques, kinematical modelling approaches are good at simulating the positions of Kikuchi bands and their overall intensities, but they are very poor at predicting the correct intensity distributions within the patterns and, consequently, do not produce realistic-looking simulations.
Dynamical pattern simulations, on the other hand, do successfully reproduce the intensity distributions within an EBSD pattern. This makes it possible to utilise mathematical image correlation techniques to determine which of a set of simulated EBSPs best matches any experimental EBSP.
The utilisation of simulated EBSD patterns for indexing requires the generation of a library, or “dictionary”, of individual pattern simulations, each of which represents a single orientation. It is usually most efficient to generate a single “master” pattern, such as is shown to the right, that contains the full range of possible crystallographic orientations, often projected onto the surface of a sphere.
From this master pattern, individual simulated EBSPs are derived, each representing a single orientation. These EBSPs make up the library of simulations, against which each experimental EBSP is correlated. The process can be very time consuming: generating the master pattern can take a number of hours, and the size of the library of simulated patterns can be extremely large and will depend on the required angular precision.
For example, for a cubic phase with a desired 1° angular precision (relatively poor compared to conventional Hough-based indexing techniques), you would need close to 1,000,000 simulated patterns in the library, and for lower crystal symmetries even greater numbers of simulated patterns are required. Once the library of patterns has been created, each experimental pattern needs to be compared to the simulated patterns: this is usually done by converting each pattern (experimental and simulated) into a normalised column vector and then using a standard dot product metric to determine the best fitting simulated pattern (and hence the orientation). An example experimental EBSP and best-fit simulation from an austenitic steel sample is shown in the image below.
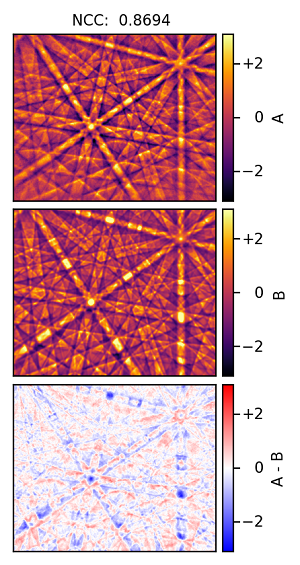
False coloured experimental EBSP (top) and best-fit simulation (centre) for an austenitic steel measurement. The lower image shows the intensity differences between the 2, with a normalised cross correlation value of 0.8694. The simulation here takes into account excess and deficit artefacts within the EBSP. Images courtesy of Aimo Winkelmann.

Dynamically simulated EBSD master pattern for austenitic steel (FCC Fe). This is a stereographic projection of the upper hemisphere simulated at 20kV with [001] at the centre. Image courtesy of Aimo Winkelmann.
The single greatest drawback of the dictionary indexing approach is the speed; it takes a long time to create the master pattern, to derive the individual simulated EBSPs, to collect (and store) the experimental patterns and then to carry out the image correlation to give the required orientation and phase information. Even then, the orientation precision is likely to be far inferior to indexing results using Hough-based techniques.
However, dictionary indexing has one significant advantage over conventional indexing: even if the EBSP quality is too poor to enable reliable Kikuchi band detection via the Hough transform, dictionary indexing will still provide robust results in most cases. This makes the technique ideal for the study of materials that are challenging to analyse using standard EBSD techniques, such as heavily deformed or nanocrystalline materials. In addition, further advances in the use of pattern simulations and pattern matching techniques enable this approach to be used to improve the quality of the indexed results (such as to eliminate pseudosymmetry-related errors or to give higher precision orientation measurements), or to extract additional information from EBSPs (such as polarity or chirality). These advances are not so much focused on the initial indexing of the patterns, but more on refining the results and are dealt with in more detail here.
Spherical indexing is a refinement to the dictionary indexing method, designed to increase the speed of analysis and therefore the usefulness of the approach. The fundamental approach of spherical indexing is the same as dictionary indexing: experimentally derived EBSD patterns are cross-correlated with a simulated diffraction pattern to determine the best fitting orientation and phase. However, the spherical master pattern (as shown in the Dictionary Indexing section, above) is correlated with a back-projected experimental pattern using the spherical harmonic transform. This approach is significantly faster than standard dictionary indexing, as there is no need to create the library of individual simulations (and hence there is no penalty for working with lower symmetry phases), yet it provides a similar quality of data in cases where the Hough-based indexing techniques fail.
Critically, spherical indexing can deliver indexing speeds that are similar to the acquisition speeds of many modern EBSD detectors. Depending on the computing hardware and the set-up of the spherical indexing parameters, analysis speeds exceeding 1000 patterns per second are attainable, making real-time indexing using this approach a possibility. Although a relatively new development, it is likely that continued advances in simulations and pattern matching techniques will make Dictionary and Spherical Indexing methods more commonplace for a range of EBSD applications in the future.