Electron Backscatter Diffraction

Pseudosymmetry Correction

Many crystal structures belong to one crystallographic symmetry group but share many characteristics with a group of higher symmetry. For example, the mineral quartz (SiO₂) is trigonal but has a structure that is close to being hexagonal. This is known as pseudosymmetry and can cause significant problems for Electron Backscatter Diffraction (EBSD) analyses. Keeping with the quartz example, the images show a typical low resolution EBSP from quartz, and 2 possible solutions, rotated 60° about the <0001> axis relative to each other.

These systematic indexing errors can usually be avoided by careful optimisation of the experimental parameters, including:

Collection of better quality EBSPs
Ensuring that the detector is positioned closer to the sample, resulting in a large solid angle
Detection of enough bands to ensure that the critical Kikuchi bands are being detected
Use of enough theoretical reflectors in the crystal structure to include the critical lattice planes

Example of EBSD pseudosymmetry for the trigonal mineral quartz showing correctly and incorrectly indexed EBSD patterns

Typical low resolution EBSD pattern from Quartz (SiO₂), with a correct (top) and incorrect (bottom) solution. The incorrect solution is rotated 60° about the <0001> axis relative to the correct solution (i.e. the <m> axis is in the place of the <a> axis) Note the presence of certain Kikuchi bands (marked with red arrows) that distinguish the correct solution from its pseudosymmetric equivalent.

EBSD orientation map showing the effects of pseudosymmetry-related misindexing in the mineral ilmenite

Orientation map showing some ilmenite (FeTiO₃) grains in a rock sample. The checkerboard / speckled appearance in some grains is caused by the pseudosymmetry of ilmenite: it is low trigonal (Laue group -3), but very close to high trigonal (-3m).

For materials such as quartz, the Tru-I class indexing algorithm will successfully resolve the trigonal symmetry of the material, minimising any systematic misindexing. However, for some materials, the pseudosymmetry can result in errors, even with optimisation of the experimental parameters, and this will lead to orientation maps that have a “checkerboard” appearance, as shown on the left.

There are 2 ways to solve these problems (unless you resort to time-consuming pattern matching techniques), and these are highlighted in the following tabs.

Pseudosymmetry Indexing Solution
Pseudosymmetry Cleanup

Within AZtecHKL, there is an optional module (“Pseudosymmetry”) that utilises pre-knowledge about potential pseudosymmetric problems to ensure correct indexing. This tool is best used with good quality EBSPs and works as follows:

For a phase with a potential pseudosymmetry problem, the user defines the nature of this pseudosymmetry. There are several ways that this can be done:

1. Using one of the predefined pseudosymmetry relationships within AZtec.
2. Utilising the measured disorientation angle and axis between correct and incorrect solutions to define the axis and fold (i.e. the rotational symmetry). In some cases, this may not fully define the pseudosymmetry for a particular phase, but will still likely provide significant benefits.
3. Determine the pseudosymmetry via a more detailed analysis of the crystallography. This may involve determining the required change in symmetry (e.g. from tetragonal 4/mmm with 8 equivalent orientations to cubic m3m with 24 equivalent orientations, a 3-fold pseudosymmetry can be defined), and can be calculated by looking at the list of all equivalent misorientations between different pseudosymmetric solutions.
AZtec will modify the reflector list to reflect the pseudosymmetry definition, ensuring that the indexing will use the higher symmetry of the pseudosymmetric structure (but with the correct d-spacing for all lattice planes)
During indexing, all equivalent pseudosymmetric solutions will be determined
With the use of refined accuracy indexing, the best fit solution will be determined from the multiple pseudosymmetric solutions, with the final indexing performed to the correct symmetry of the phase

There are limitations to this approach: the EBSP quality cannot be too poor (as the differences between the pseudosymmetric equivalents needs to be resolved), and the difference between the structures has to be sufficient: typically at least 1-2% difference.

The efficacy of this approach is shown in the following example. The phase γ-TiAl is tetragonal, but the c:a ratio is only 1.018, so it is very close to having a cubic structure. With conventional indexing (the left-hand image), the orientation map has the characteristic checkerboard or speckled appearance, indicating that the indexing algorithm struggles to differentiate between 2 or more solutions. When the Pseudosymmetry tool is enabled within AZtec in conjunction with the refined accuracy indexing mode (using a 3-fold relationship close to the <111> axis), as shown in the right image, the indexing is far more robust, and the detailed structures of the twins in this material are fully resolved.

EBSD orientation maps from gamma TiAl showing how AZtec’s pseudosymmetry tool enables error-free mapping of the twins

Example orientation maps from γ-TiAl collected using standard indexing (left) and with a combination of refined accuracy and pseudosymmetry definitions in AZtec (right)

Further details about this application can be read in our detailed application note, available here.

In many cases the degree of pseudosymmetry-related misindexing is relatively minor, and only becomes apparent once the data collection has been completed. In this situation it is possible to clean up the pseudosymmetric errors during the data analysis process.

This process can be carried out using AZtecCrystal and follows these steps:

Identify the pseudosymmetric relationship (i.e. the rotation angle and axis between correct solutions and pseudosymmetric errors in the map). This can be carried out using the “Measure” tool in AZtecCrystal, and the relationship appended directly to the data clean-up routines.
In the data clean-up viewing mode, either define the known pseudosymmetry relationship or load it from a predefined database (or it can be preloaded based on a prior measurement using the Measure tool, as described in (1)).
If necessary, set the maximum domain size (in pixels) that should be corrected. This is relevant when correcting datasets that have twin domains with the same crystallographic relationship as the pseudosymmetry indexing problems: domains larger than the defined area are considered to be genuine twins and not indexing errors and are left untouched.
The software will rotate the pseudosymmetric errors into coincidence with the rest of the grain based on the defined crystallographic relationship.

This process is demonstrated in the following dataset from a quartz rock, showing how isolated pseudosymmetry errors can be removed whilst retaining genuine twin boundaries with the same crystallographic relationship.

IPF orientation maps of a quartz rock collected at high speed (>1600 patterns per second)

EBSD orientation map showing minor misindexing in the mineral quartz, along with Dauphine twins

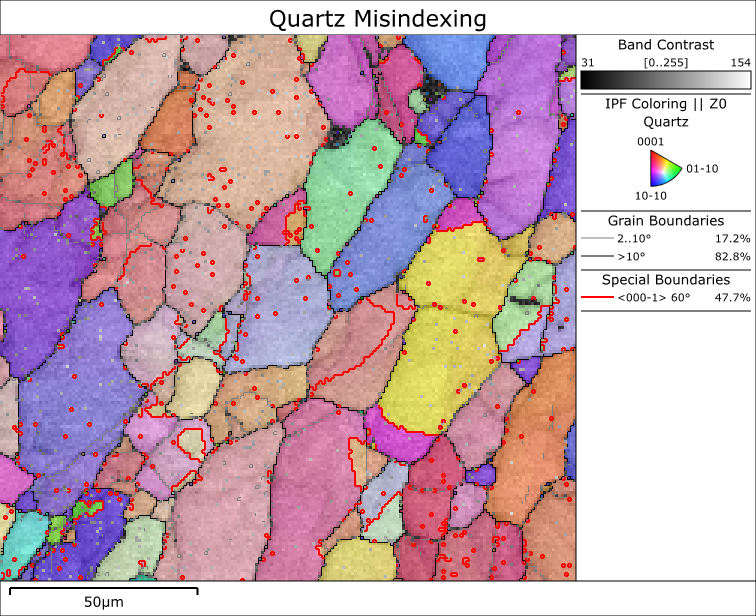
The raw data shows that some grains contain isolated indexing errors caused by the pseudo-hexagonal structure of quartz. These are shown as isolated pixels or groups of pixels with red borders (denoting a 60° rotation about <0001>). However, also present are “Dauphiné Twins” that have the same crystallographic relationship.

EBSD orientation map of quartz following the removal of pseudosymmetry-related errors using AZtecCrystal

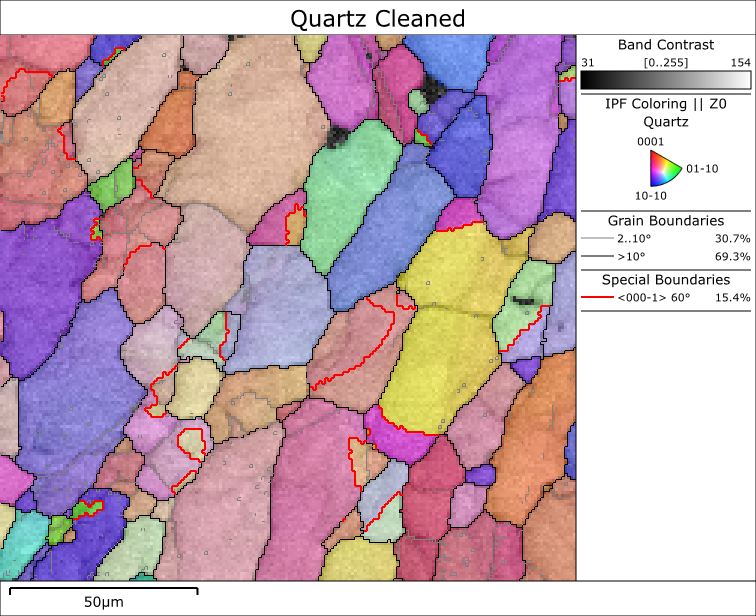
The IPF map shows the data after cleaning to remove pseudosymmetric errors but retaining any twin domains >10 pixels in area. This process will then enable a more accurate analysis of the quartz boundary populations and the extent of Dauphiné Twinning in the sample.

Related Products

Website by Miramar Communications Ltd